En attendant les pièces pour le rabot, on se prépare à travailler la couture. Parmi ces travaux : la réalisation des patrons. Globalement c'est relativement simple, puisque la yourte a une géométrie simple. Toutefois, le cas du tronc de cône qui nous sert de toiture mérite probablement une petite explication.

Les méandres de la géométrie

D'abord, il faut remarquer qu'un tronc de cône est une surface sans courbure. Ça ne signifie pas que c'est « droit ». Ça signifie, pour faire simple, qu'on peut y appliquer les règles de la géométrie euclidienne, celle qu'on a apprise à l'école. Par exemple, celle qui dit que la somme des angles d'un triangle fait 180° en géométrie euclidienne.

Ce n'est pas une vérité générale. Essayez par exemple de couper une orange selon deux méridiens perpendiculaires et selon l'équateur ; de façon à obtenir un huitième d'orange. Vous constaterez facilement que vous aurez découpé sur la sphère un triangle à trois angles droits !

Heureusement pour nous, le cône est plus simple. Comme le cylindre, le cône est une surface sans courbure. C'est pour ça qu'on peut facilement coller des étiquettes sur les bouteilles de Bordeaux. Et c'est aussi pour ça que, ô bonne nouvelle, on peut recouvrir sans trop d'effort notre toit avec une pièce de tissu.

Si toutefois vous préférez les géométries torduescourbes, je vous conseille de vous munir d'un tube d'aspirine et de partir à la découverte des aventures d'Anselme Lanturlu.

Faire rentrer un cercle dans un carré de tissu

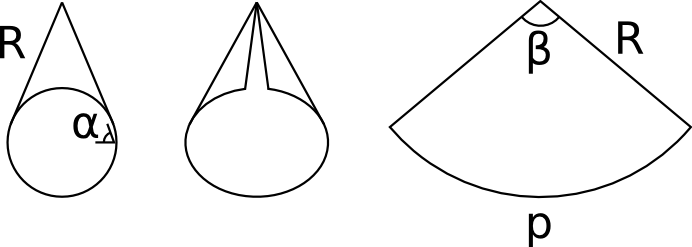
Quand on ouvre un cylindre dans la longueur et qu'on étale la matière qui le constitue, on peut l'aplatir complètement, pour former un genre de parallélogramme (ça dépend de la découpe…). C'est pareil dans le cas du cône. Commençons par supposer disposer de notre pièce de tissu finie. Découpons la le long d'un rayon et étalons le tissu. On constate bien que la chose se met à plat, pour former un genre de disque partiellement ouvert.

Il y a alors deux grandeurs qui caractérisent ce disque. Par exemple son rayon, et le taux de fermeture (i.e. la portion de tour où la matière est présente). Ou, plus pratique dans notre situation, le rayon du disque (R) et le périmètre extérieur de la portion de disque (p).

Si on recouvre notre cône initial avec ce tissu, on peut remarquer que :

• le rayon R correspond à l'apothème du cône, c'est à dire la distance entre le sommet et n'importe quel point de la base ;
• le périmètre (p) correspond au périmètre du cercle de base.

Supposons maintenant qu'on veuille obtenir les grandeurs p et R à partir de la géométrie suivante de notre cône, donnée par :

• son rayon de base r ;
• la pente de la toiture α (prononcée « alpha »).

Alors :

1. du rayon de la base r on déduit le périmètre p = 2πr ;
2. du rayon r et de la pente α on déduit l'apothème R en faisant intervenir l'ami Pythagore : R = √(r² + α²r²) ;
3. Pour faciliter le dessin on peut aussi connaitre l'angle au centre : β = 360*r/R.

Conclusion

Et voilà ! Pour faire un patron complet, il restera à lui soustraire la partie supérieure du toono, à diviser la forme obtenue en morceaux plus petits, et à ajouter les valeurs de coutures nécessaires aux assemblages.